Poissonian Distribution in Quantum Optics

Understanding how light behaves at the quantum level is crucial in quantum optics. One fundamental concept that aids in this understanding is the Poissonian distribution. This statistical tool helps scientists and engineers predict how photons, the basic units of light, are distributed in various light sources.

What is Poissonian Distribution?

The Poisson distribution helps determine how likely it is for a number of events to occur within a fixed duration or area, assuming the events are random, unrelated, and occur at a steady rate with a known constant mean rate and independently of the time since the last event. In quantum optics, this translates to predicting the likelihood of detecting a certain number of photons in a given time frame.
Mathematically, the probability P(𝑛) of detecting 𝑛 photons is given by:

P(𝑛)=𝑛!⟨𝑛⟩𝑛e−⟨𝑛⟩​

Here, ⟨𝑛⟩ represents the average number of photons detected.​

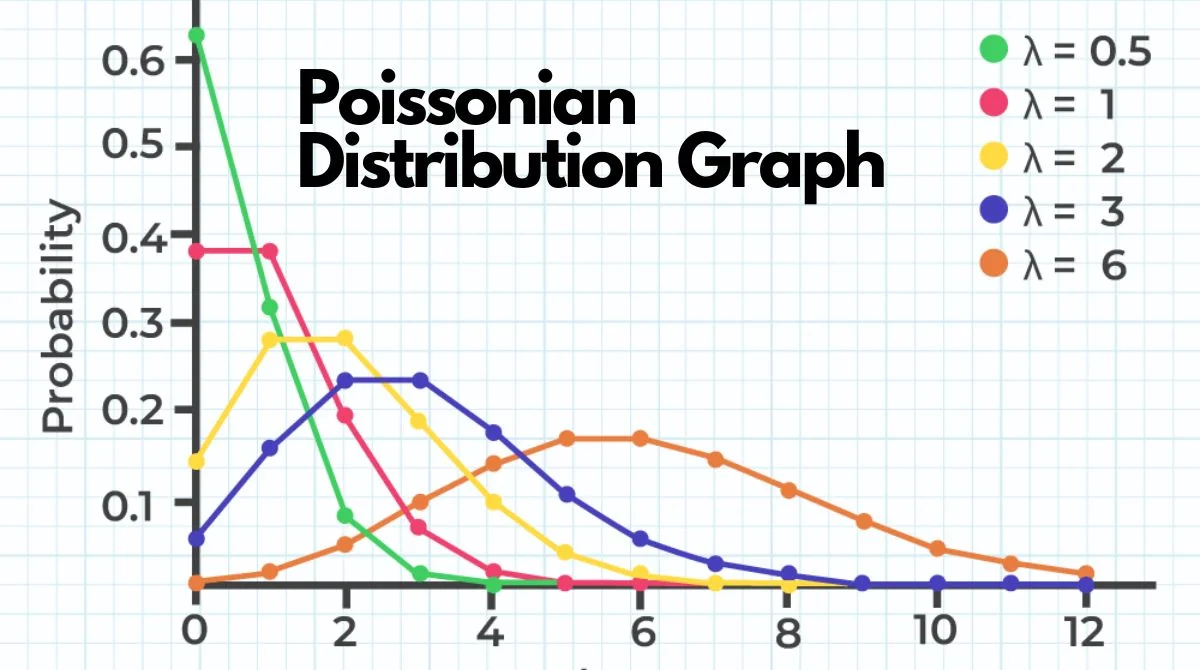
Coherent Light and Poissonian Statistics

Light from perfectly coherent sources, such as an ideal laser, maintains uniform phase and intensity over time. In such cases, the photon distribution follows the Poissonian model. This means that the variance (a measure of spread) in the number of detected photons equals the mean number of photons. This property is a hallmark of coherent states in quantum optics.

For example, if an average of 10 photons is detected per interval, the standard deviation (a measure of fluctuation) is approximately 3.16, which is the square root of 10. This relationship indicates that as the average number of photons increases, the relative fluctuation decreases, leading to more stable light intensity.

Comparing Photon Statistics

Photon statistics can be categorized based on the relationship between the variance and the mean:

• Poissonian: Variance equals the mean. Characteristic of coherent light sources like lasers.
• Sub-Poissonian: Variance is less than the mean. Indicates non-classical light with reduced noise, useful in quantum technologies.
• Super-Poissonian: Variance exceeds the mean. Typical of thermal or chaotic light sources, such as incandescent bulbs.

Understanding these distinctions is vital for applications that require precise control over light properties.

Applications in Quantum Technologies

The Poissonian distribution plays a significant role in various quantum technologies:

• Quantum Cryptography: In quantum key distribution (QKD), attenuated laser pulses are used to send information securely. These pulses often follow Poissonian statistics, which is crucial for ensuring the security of the communication.
• Quantum Imaging: Techniques like quantum imaging rely on understanding photon statistics to enhance image resolution beyond classical limits.
• Photon Detection: Accurate photon counting, essential in many quantum experiments, depends on the statistical models provided by the Poissonian distribution.

Mandel Q Parameter

To quantify deviations from Poissonian statistics, the Mandel Q parameter is used:

Q=⟨n⟩⟨(Δn)2⟩−⟨n⟩​

• Q=0: Poissonian distribution.
• Q<0: Sub-Poissonian (reduced noise)
• Q>0: Super-Poissonian (increased noise)

This parameter helps in identifying the nature of the light source and its suitability for specific quantum applications.

Real-World Implications

Understanding Poissonian distribution is not just theoretical; it has practical implications:

• Designing Light Sources: Engineers can design lasers and other light sources with desired statistical properties for specific applications.
• Improving Measurement Accuracy: In experiments where precise photon counting is essential, knowing the expected distribution aids in reducing errors.
• Enhancing Communication Security: Quantum communication protocols rely on predictable photon statistics to detect eavesdropping and ensure secure information transfer.

Measurement Techniques for Photon Statistics

To study whether a light source follows Poissonian statistics, scientists use various photon detection methods. These techniques help analyze how photons arrive over time and whether they match the predicted statistical models. Here are some commonly used methods:

• Single-Photon Avalanche Diodes (SPADs): These are highly sensitive detectors that can register single photons. They are fast and suitable for counting photons in real time, making them ideal for testing Poissonian behavior.
• Photomultiplier Tubes (PMTs): PMTs amplify the signal from incoming photons, allowing detection of very weak light. They are often used in experiments where high sensitivity is more important than perfect accuracy in photon counting.
• Time-Correlated Single Photon Counting (TCSPC): It is a method used to record photon arrival times with exceptionally high accuracy. It’s widely used in quantum optics to study the timing and statistical spread of photons.
• Hanbury Brown and Twiss (HBT) Setup: This is a classic setup used to measure second-order coherence. It helps determine whether a source is Poissonian, sub-Poissonian, or super-Poissonian by analyzing photon correlations.

These techniques are essential for confirming the statistical nature of light in both research and application settings. Choosing the right method depends on the specific requirements of the experiment, whether it’s timing accuracy, sensitivity, or photon number resolution.

Poissonian Light in Practical Quantum Devices

In the world of quantum optics, understanding the nature of photons is essential when designing any device or system. The Poissonian distribution plays a central role here. It is especially useful when analyzing light sources that emit coherent light, such as ideal lasers.

Today, several real-world quantum devices rely on Poissonian photon behavior to function properly. Here are some examples where Poissonian light is important:

• Laser Sources in Quantum Experiments: Lasers that closely follow Poissonian photon statistics are often used as reference sources in labs. They help researchers understand what kind of photon fluctuations are expected under ideal conditions.
• Photon-Based Quantum Computers: In some quantum computing platforms, photons act as carriers of information. If these photons behave in a Poissonian manner, it makes the system design more predictable and helps with error correction.
• Quantum Sensors: Highly sensitive quantum sensors often rely on Poissonian light as a baseline. Because the fluctuations are mathematically predictable, it becomes easier to spot actual signal changes versus noise.
• Metrology and Calibration Tools: Devices that measure the intensity or stability of light use Poissonian light as a standard. Since the distribution is well understood and stable, it simplifies the calibration process.

In all these cases, Poissonian behavior acts like a signal of reliability. If a light source shows Poissonian distribution, it usually means the light is coherent, stable, and predictable, which is exactly what is needed in precision quantum technologies.

Conclusion

The Poissonian distribution is a fundamental concept in quantum optics, providing a framework to understand and predict photon behavior in various light sources. Its applications span from secure communications to advanced imaging techniques, making it an indispensable tool in the advancement of quantum technologies.